Autobatching for Bayesian Inference#
This notebook demonstrates a simple Bayesian inference example where autobatching makes user code easier to write, easier to read, and less likely to include bugs.
Inspired by a notebook by @davmre.
import functools
import itertools
import re
import sys
import time
from matplotlib.pyplot import *
import jax
from jax import lax
import jax.numpy as jnp
import jax.scipy as jsp
from jax import random
import numpy as np
import scipy as sp
Generate a fake binary classification dataset#
np.random.seed(10009)
num_features = 10
num_points = 100
true_beta = np.random.randn(num_features).astype(jnp.float32)
all_x = np.random.randn(num_points, num_features).astype(jnp.float32)
y = (np.random.rand(num_points) < sp.special.expit(all_x.dot(true_beta))).astype(jnp.int32)
y
array([0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0,
1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0,
1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0,
0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1,
1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0], dtype=int32)
Write the log-joint function for the model#
We’ll write a non-batched version, a manually batched version, and an autobatched version.
Non-batched#
def log_joint(beta):
result = 0.
# Note that no `axis` parameter is provided to `jnp.sum`.
result = result + jnp.sum(jsp.stats.norm.logpdf(beta, loc=0., scale=1.))
result = result + jnp.sum(-jnp.log(1 + jnp.exp(-(2*y-1) * jnp.dot(all_x, beta))))
return result
log_joint(np.random.randn(num_features))
Array(-213.2356, dtype=float32)
# This doesn't work, because we didn't write `log_prob()` to handle batching.
try:
batch_size = 10
batched_test_beta = np.random.randn(batch_size, num_features)
log_joint(np.random.randn(batch_size, num_features))
except ValueError as e:
print("Caught expected exception " + str(e))
Caught expected exception Incompatible shapes for broadcasting: shapes=[(100,), (100, 10)]
Manually batched#
def batched_log_joint(beta):
result = 0.
# Here (and below) `sum` needs an `axis` parameter. At best, forgetting to set axis
# or setting it incorrectly yields an error; at worst, it silently changes the
# semantics of the model.
result = result + jnp.sum(jsp.stats.norm.logpdf(beta, loc=0., scale=1.),
axis=-1)
# Note the multiple transposes. Getting this right is not rocket science,
# but it's also not totally mindless. (I didn't get it right on the first
# try.)
result = result + jnp.sum(-jnp.log(1 + jnp.exp(-(2*y-1) * jnp.dot(all_x, beta.T).T)),
axis=-1)
return result
batch_size = 10
batched_test_beta = np.random.randn(batch_size, num_features)
batched_log_joint(batched_test_beta)
Array([-147.84033 , -207.02205 , -109.26075 , -243.80833 , -163.0291 ,
-143.84848 , -160.28773 , -113.771706, -126.60544 , -190.81992 ], dtype=float32)
Autobatched with vmap#
It just works.
vmap_batched_log_joint = jax.vmap(log_joint)
vmap_batched_log_joint(batched_test_beta)
Array([-147.84033 , -207.02205 , -109.26075 , -243.80833 , -163.0291 ,
-143.84848 , -160.28773 , -113.771706, -126.60544 , -190.81992 ], dtype=float32)
Self-contained variational inference example#
A little code is copied from above.
Set up the (batched) log-joint function#
@jax.jit
def log_joint(beta):
result = 0.
# Note that no `axis` parameter is provided to `jnp.sum`.
result = result + jnp.sum(jsp.stats.norm.logpdf(beta, loc=0., scale=10.))
result = result + jnp.sum(-jnp.log(1 + jnp.exp(-(2*y-1) * jnp.dot(all_x, beta))))
return result
batched_log_joint = jax.jit(jax.vmap(log_joint))
Define the ELBO and its gradient#
def elbo(beta_loc, beta_log_scale, epsilon):
beta_sample = beta_loc + jnp.exp(beta_log_scale) * epsilon
return jnp.mean(batched_log_joint(beta_sample), 0) + jnp.sum(beta_log_scale - 0.5 * np.log(2*np.pi))
elbo = jax.jit(elbo)
elbo_val_and_grad = jax.jit(jax.value_and_grad(elbo, argnums=(0, 1)))
Optimize the ELBO using SGD#
def normal_sample(key, shape):
"""Convenience function for quasi-stateful RNG."""
new_key, sub_key = random.split(key)
return new_key, random.normal(sub_key, shape)
normal_sample = jax.jit(normal_sample, static_argnums=(1,))
key = random.key(10003)
beta_loc = jnp.zeros(num_features, jnp.float32)
beta_log_scale = jnp.zeros(num_features, jnp.float32)
step_size = 0.01
batch_size = 128
epsilon_shape = (batch_size, num_features)
for i in range(1000):
key, epsilon = normal_sample(key, epsilon_shape)
elbo_val, (beta_loc_grad, beta_log_scale_grad) = elbo_val_and_grad(
beta_loc, beta_log_scale, epsilon)
beta_loc += step_size * beta_loc_grad
beta_log_scale += step_size * beta_log_scale_grad
if i % 10 == 0:
print('{}\t{}'.format(i, elbo_val))
0 -180.8538818359375
10 -113.06045532226562
20 -102.73727416992188
30 -99.787353515625
40 -98.90898132324219
50 -98.29745483398438
60 -98.18632507324219
70 -97.57972717285156
80 -97.28599548339844
90 -97.46996307373047
100 -97.4771728515625
110 -97.5806655883789
120 -97.4943618774414
130 -97.50271606445312
140 -96.86396026611328
150 -97.44197845458984
160 -97.06941223144531
170 -96.84028625488281
180 -97.21336364746094
190 -97.56503295898438
200 -97.26397705078125
210 -97.11979675292969
220 -97.39595031738281
230 -97.16831970214844
240 -97.118408203125
250 -97.24345397949219
260 -97.29788970947266
270 -96.69286346435547
280 -96.96438598632812
290 -97.30055236816406
300 -96.63591766357422
310 -97.0351791381836
320 -97.52909088134766
330 -97.28811645507812
340 -97.07321166992188
350 -97.15619659423828
360 -97.25881958007812
370 -97.19515228271484
380 -97.13092041015625
390 -97.11726379394531
400 -96.938720703125
410 -97.26676940917969
420 -97.35322570800781
430 -97.21007537841797
440 -97.28434753417969
450 -97.1630859375
460 -97.2612533569336
470 -97.21343994140625
480 -97.23997497558594
490 -97.14913940429688
500 -97.23527526855469
510 -96.93419647216797
520 -97.21209716796875
530 -96.82575988769531
540 -97.01284790039062
550 -96.94175720214844
560 -97.16520690917969
570 -97.29165649414062
580 -97.42941284179688
590 -97.24370574951172
600 -97.15222930908203
610 -97.49844360351562
620 -96.9906997680664
630 -96.88956451416016
640 -96.89968872070312
650 -97.13793182373047
660 -97.43705749511719
670 -96.99235534667969
680 -97.15623474121094
690 -97.1869125366211
700 -97.11160278320312
710 -97.78105163574219
720 -97.23226165771484
730 -97.16206359863281
740 -96.99581909179688
750 -96.6672134399414
760 -97.16795349121094
770 -97.51435089111328
780 -97.28900146484375
790 -96.91226196289062
800 -97.17100524902344
810 -97.29047393798828
820 -97.16242980957031
830 -97.19107055664062
840 -97.56382751464844
850 -97.00194549560547
860 -96.86555480957031
870 -96.76338195800781
880 -96.83660888671875
890 -97.12178039550781
900 -97.09554290771484
910 -97.0682373046875
920 -97.11947631835938
930 -96.87930297851562
940 -97.45624542236328
950 -96.69279479980469
960 -97.29376220703125
970 -97.3353042602539
980 -97.34962463378906
990 -97.09675598144531
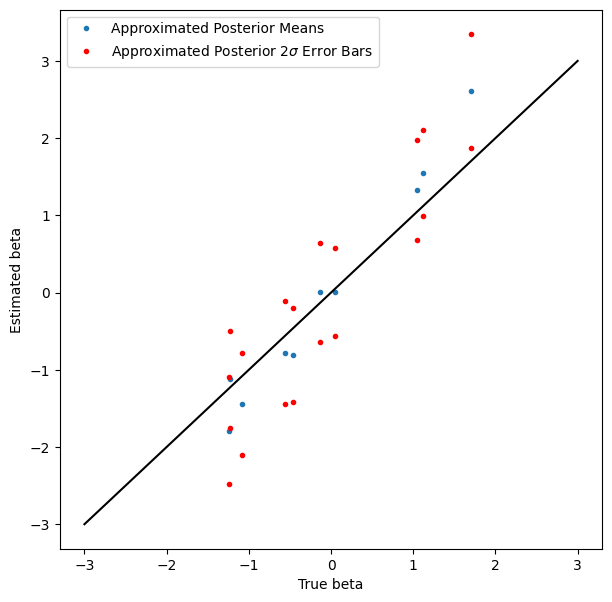
Display the results#
Coverage isn’t quite as good as we might like, but it’s not bad, and nobody said variational inference was exact.
figure(figsize=(7, 7))
plot(true_beta, beta_loc, '.', label='Approximated Posterior Means')
plot(true_beta, beta_loc + 2*jnp.exp(beta_log_scale), 'r.', label='Approximated Posterior $2\sigma$ Error Bars')
plot(true_beta, beta_loc - 2*jnp.exp(beta_log_scale), 'r.')
plot_scale = 3
plot([-plot_scale, plot_scale], [-plot_scale, plot_scale], 'k')
xlabel('True beta')
ylabel('Estimated beta')
legend(loc='best')
<matplotlib.legend.Legend at 0x7ff82242f730>